From the genetic lottery we're thrown into at birth, to the educational opportunities we navigate, the jobs we compete for, and the relationships we cultivate—every stage in life is marked by wins and losses, strategies and tactics, alliances, and competition. But not all games are zero-sum showdowns. To understand non-zero-sumness it helps to consider "sum" different types of games.
- zero-sum games
- positive-sum games
- negative-sum games
- meta-games
... are where two parties compete and in order for one party to win the other must lose. The positive payoff for the winner in such a game requires an equally negative payoff for the loser, so that the sum of the payoff is zero, hence "zero-sum". Chess is as zero-sum game because players can't both win or both lose, so is soccer... or competitive eating.
There are also lots of common sense sayings that echo zero-sum thinking 'You don't get something for nothing', 'you get what you pay for' or 'you can't have your cake and eat it too'. Like any well-designed memes, these sayings have survived because in many situations they are confirmed by experience, but not always.
With non-zero-sum games, while you may not get something for nothing, the whole can be greater than the sum of its parts.
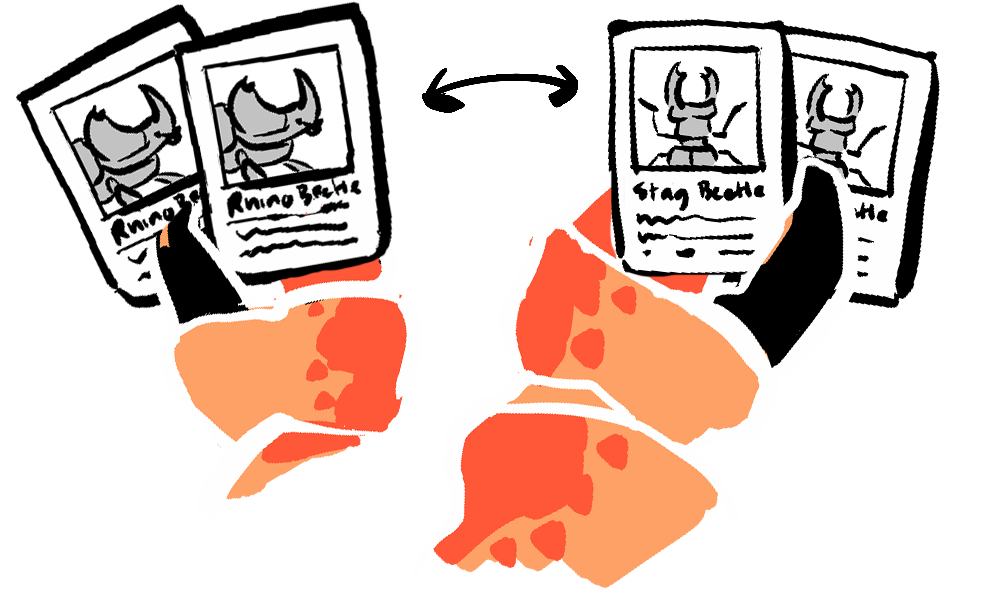
... are non-zero-sum games which result in win-win scenarios. Imagine two card collectors who each have doubles of cards that the other doesn't have. Swapping their doubles leaves both closer to completing their collection.
This kind of game is generally what people (and this website) mean when talking about a non-zero-sum game.

Later on we'll get to an example where the stakes are slightly higher than an incomplete card collection.
... are another type of non-zero-sum game, the flip-side of positive-sum games where both sides lose. Like a bar-room brawl with even odds, there are just going to be a lot of injuries and property damage.
Identifying negative-sum games (and avoiding them) can often be as beneficial as taking part in positive-sum games.
AN EXAMPLE FROM NATURE
Interestingly, nature has found ways around negative-sum games, by animals evolving behaviours or physical attributes that are demonstrative of dominance, rather than having to physically fight one another. Take for instance those weird horned beetles you've seen, the Hercules or Rhinoceros Beetle or the Stag Beetle with its over-sized mandibles. Not only does the "size of their horn" matter for sexual selection, but also for asserting dominance over competitive males without the need for physical conflict.

In fact even when they fight, these beetles do so without injury, generally by flipping their opponent off whatever branch they're on.
Humans also take part in elaborate exercises that help us steer clear of conflict. Imagine the wars we've avoided by having a small group of elite sports people compete for the pride of their nation. And more explicitly, the acknowledgement of "Mutually Assured Destruction" has so far played a key role in avoiding the very negative-sum game of thermo-nuclear war.
... are wider games in which other games are embedded, meaning that zero-sum games can become part of larger non-zero-sum systems. This is where we venture away from the well-bounded world of Game Theory into the messy real world, and things get really interesting.
It's sports analogy time!!!.
The 'SOUP-A-BOWL' is an international soup-eating competition—a winner-takes-all game between the competitive-eating elite from across the globe, a very zero-sum game. But surrounding the game is an entire industry made up of...
- Fans—who pay to get entertainment that they find more valuable than the cost of the ticket
- A Stadium—that gets more from ticket sales than the cost associated with the event
- Competitors—who get to eat all they want and enjoy the prestige of representing their country
- Sponsors—who get exposure for their products while also competing to make the most entertaining adverts that are eagerly anticipated by fans as part of the spectacle.
At each meta-level of the competition there are accumulative win-win (positive-sum) games, transforming a zero-sum game into a whole non-zero-sum system.

... in essense, non-zero-sum games are any situation where a positive payoff for a winner doesn't necessarily require an equally negative payoff for the loser. Non-zero-sum games are interactions that can be positive for everyone (a positive-sum game) or conversely, negative for all parties (a negative-sum game). But most interestingly, understanding non-zero-sumness can help us look at the complex multi-layered games (meta-games) that arise in our everyday lives, so we can better decide which games to create and play and which we might prefer to avoid.