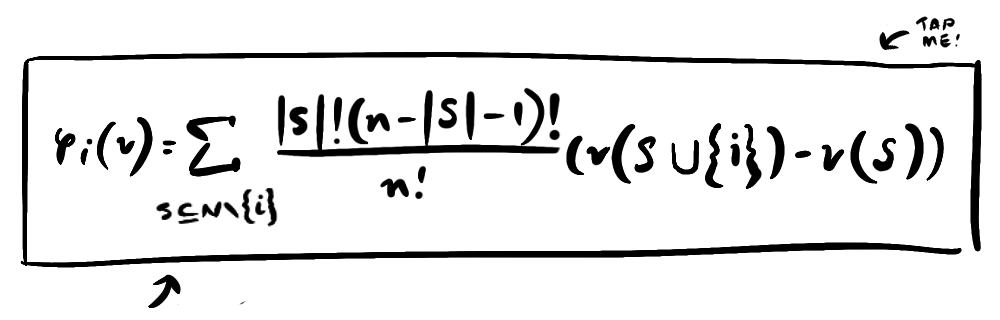

In non-zero-sum games, individuals can work together to achieve a result that's greater than the sum of their parts—which is great. But what happens when it comes to divvying up those gains, if some players have contributed more than others?
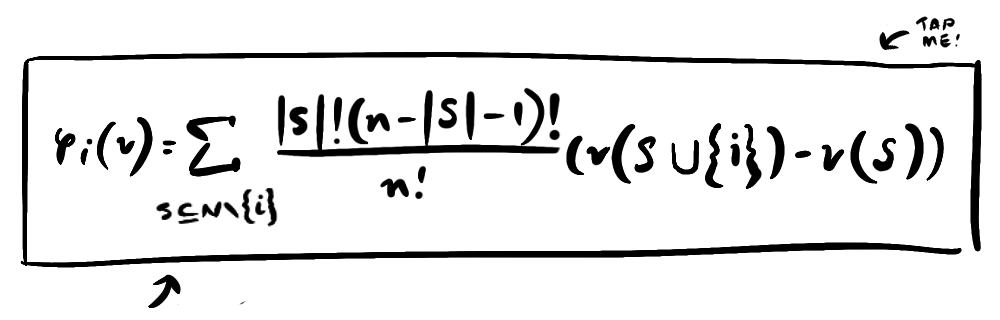
This is the Shapley Value—a method in Game Theory to fairly distribute the total gains or costs among players, based on their contributions. Previously, I've dismissed this convoluted formula as ridiculous. But, given it did win Lloyd Shapley a Nobel Prize, I've created a Shapley Value calculator to demystify this enigmatic algorithm.
First let's try to understand it in plain english.
My Shapley Value = Sum of (Weight x Each of my marginal contributions)... or in more detail...
Sum of ( Number of ways I can join a coalition Total number of possible coalitions x (Each coalition's value with me - without me))
A player's marginal contribution to a is the difference between the value of the coalition with and without them. So, if a coalition is worth $70 with a given player and $30 without, that player's marginal contribution is $40
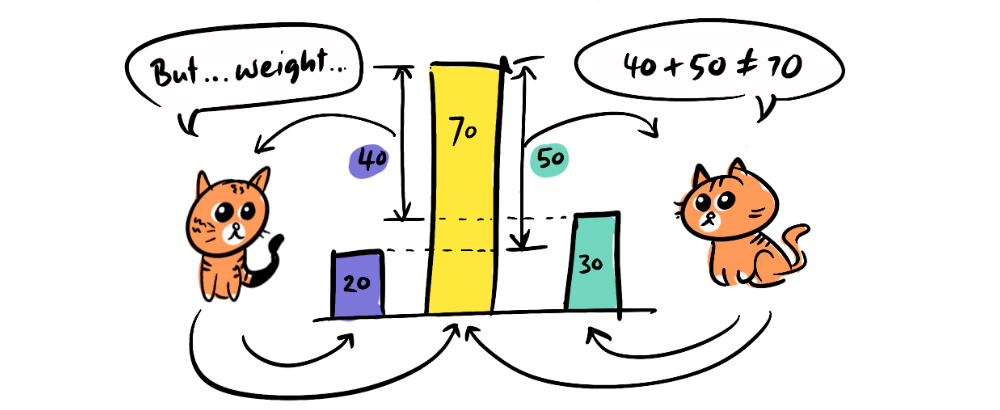
But wait, let's say we have two players who, working alone, can each generate a $20 and $30 payoff respectively, but together can make $70, that means that the first player makes a marginal contribution $40, while the other makes a marginal contribution of $50. That doesn't work, right? They can't both claim their marginal contributions because they've only generated $70 between them (their marginal values overlap).
This is where we have to use...

In order to apportion a player's marginal contribution correctly, we divide each of their marginal contributions by the number of coalitions they can join. This gives us their weighted marginal contributions. Add these all up, and you have their Shapley Value—their fair share of the payoff from the .
Let's go through a scenario, this could be sharing the cost savings of sharing a taxi, or sharing the profits of a joint investment, Shapley Value works for both.